Probability in itself is a huge topic to study. Applications of probability are found everywhere whether it is medical science, share market trading, sports, gaming Industry and many more. However in this post my focus is on to explain the topics which are needed to understand data science and machine learning concepts.
Table of Content:
- Probability
- Sample Space
- Event
- Probability vs Statistics
- Mutually Exclusive events
- Independent Events
- Joint Probability
- Union Probability
- Marginal Probability
- Examples
There are other advance topics like Conditional Probability, Bayes’ Theorem and Probability distribution which I will be explaining in next post. As these are very important concepts and need more understanding and hence I will dedicate separate article for each of those topics. For now let’s concentrate on basic probability as mentioned in the table of contents above.
What is Probability?
In simplest terms, probability is all about the guess work. When we apply our common sense and guess the possible outcome of an event. In other terms, when we ask ourselves, what are the chances, to get a desired outcome from a sample space? These no of chances are known as probability of that desired outcome. But when it comes to Math, how are we going to calculate those chances. Here mathematicians have defined certain formula to get the probability.
“Probability is a measure quantifying the likelihood that events will occur.” – Wikipedia
Probability is the ratio of favourable or expected outcomes to the total no of possible outcomes.
If the we denote the expected outcome as n(E) and total possible outcomes as n(S). Then probability of getting an outcome “A” from total sample space S is
P(A) = n(E)/n(S)
Sample Space: Set of all possible outcomes denoted by S.
Event: A subset of the sample space.
Probability vs Statistics
Probability is used to predict the likelihood of the future event.
Statistics is used to analyse the past events
Also,
Probability tells us what will happen in a given ideal world?
While Statistics tells about how ideal is the world?
Probability is the basics of Inferential Statistics.
Assigning Probabilities
1. Classical Method: A Priori or Theoretical
Probability can be determined prior to conducting any experiment.
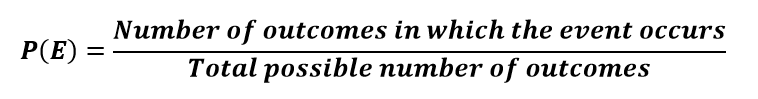
Example: Tossing of a fair die.
Here total possible outcomes = 6. And each digit appears only once in a die so when we toss, only one digit can appear in top.
So P(E) = 1/6
2. Empirical Method: A Posteriori or Frequentist
Probability can be determined post conducting a thought experiment.

Example: Tossing of a weighted die…well! Even a fair die.
The larger the number of experiments, the better the approximation. This is the most used method in statistical inference.
A fair dice is thrown two times. What is the probability that the second toss results in a value that is higher than the first toss?
P(D2 > D1) = P( D1 = 1) P( D2 > 1) + P( D1 = 2) P( D2 > 2) + P( D1 = 3) P( D2 > 3) + P( D1 = 4) P( D2 > 4) + P( D1 = 5) P( D2 > 5)
P(D1 = 1) = P(D1 = 2) = P(D1 = 3) = P(D1 = 4) = P(D1 = 5) = P(D1 = 6) = 1/6
D2>1 = (Either of the digit 2, 3, 4, 5, 6) hence 5 outcomes possible for the event to be success. Hence P(D2 > 1) = 5/6.
Similar for D2 > 2 there are 4 success scenarios either of the digit from 3,4,5,6 Hence P(D2>2) = 4/6. Similarly we can calculate other probabilities.
And now putting together
P(D2 > D1)= (1/6)*(5/6) + (1/6)*(4/6) + (1/6)*(3/6) + (1/6)*(2/6) + (1/6)*(1/6)
= (5 + 4 + 3 + 2 + 1) / 36
= 0.4167
Mutually Exclusive events
Two events A and B are said to be mutually exclusive or disjoint if both of them cannot occur at the same time. Means if A occur then B will not.
For mutually exclusive event P(A and B) = 0.
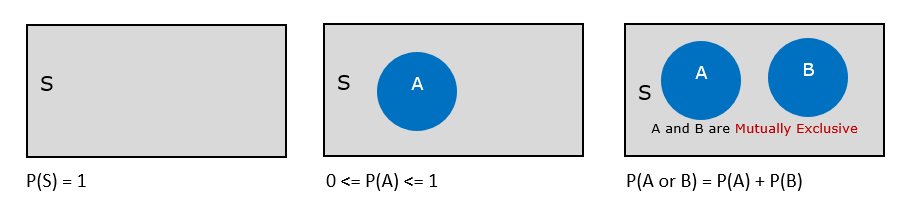
Area of the rectangle denotes sample space, and since Probability is associated with area, it cannot be negative.
Example – Mutually Exclusive Event
Tossing a fair coin. At a time only head or tail will come. Hence these events P(Head) and P(Tail) are mutually exclusive.
Note: If two events are not mutually exclusive then P(A or B) = P(A) + P(B) – P(A and B) as P(A and B) = 0 for mutually exclusive events.
Example – Not Mutually Exclusive Event
Event A – Customers who default on loans.
Event B – Customers who are High Net worth Individuals.
Here Event A and B are not mutually exclusive as both of them can occur together mean customer who are high net worth can also be loan defaulters.
Independent Events
Outcome of event A does not depend on outcome of event b and vice versa.
P(A and B) = P(A)*P(B)
Example: Independent Event
1. There are two customer A and B. Then probability of customer A defaulting on Loan is not dependent on probability of customer B defaulting on Loan.
2. If the probability of getting an interview call is 0.7, what is the probability that the next 3 calls will be for interview?
P (InterviewCall1 and InterviewCall2 and InterviewCall3) = 0.7*0.7*0.7 = 0.347
You see probability reduced, and it seems fair enough as how many times in real life we experience 3 back to back call for interview.
Another Example
A basketball team is down by 2 points with only a few seconds remaining in the game. Given that:
• Chance of making a 2-point shot to tie the game = 50%
• Chance of winning in overtime = 50%
• Chance of making a 3-point shot to win the game = 30%
What should the coach do: go for 2-point or 3-point shot? What are the assumptions, if any?
Scinerio1: Team goes for 2 point shot then
P(winning the game) = P(2 Point shot) * P(winning in overtime)
As going for the 2-point shot and winning in overtime are two independent events hence multiplying to get the probability of winning the game.
P( winning the game) =1/2 * 1/2 = ¼ =0.25
Scinerio2: Team goes for 3 point shot then
P(winning the game) = 1/3=0.33
Now we can see that going for 3-point shot is better as it has high probability associated for winning the game.
Next topic is probability Types. To understand different types, let me take an example and will try to understand with the help of this example.
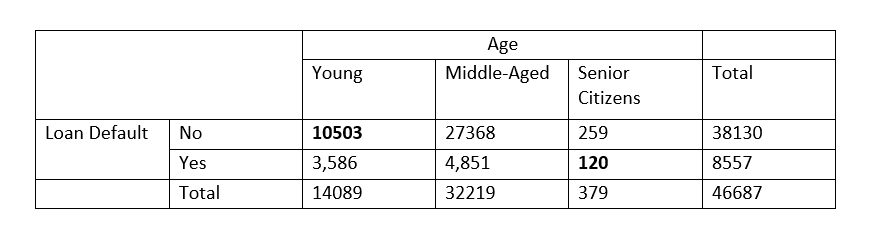
P(Young and Not Defaulting on the loan) = 10503/46687 = 0.225
P(Senior Citizens and Defaulting on loan) = 120/46687 = 0.00257 ~ 0.003
Converting the above table into probabilities
Now let’s understand Probability types.
Probability Types:
1. Joint Probability:
Joint probability defines the “AND” relationship. Probability of (A and B).
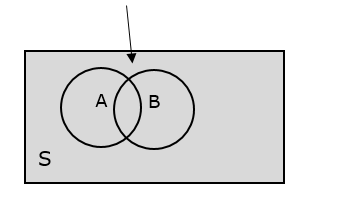
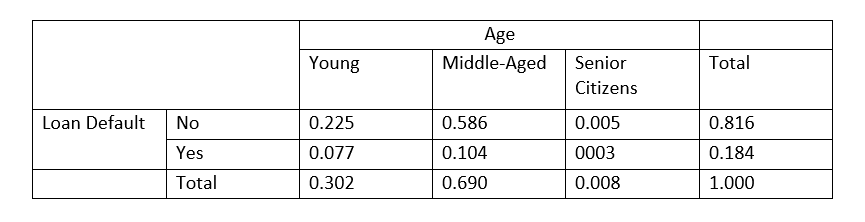
P(Yes and Young) = 0.077, P(No and Middle-Aged) = 0.586
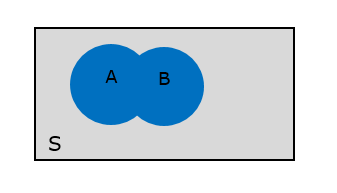
2. Union Probability
Union Probability defines the “OR” relationship. Probability of (A or B).
P(Yes or Young) = P(Yes) + P (Young) – P(Yes and Young) = 0.184 + 0.302 – 0.077 = 0.409
3. Marginal Probability
Probability describing a single attribute.
P(No) = 0.816
P(Senior Citizens) = 0.008
Conditional Probability
This topic requires detailed explanation, So I have written a separate post for this. Please refer this link: conditional probability explained with example.
Examples

In Recent Elections:
Donald Trump and Ted Cruz were Republican Party candidates. [Pic 1]
Hillary Clinton and Bernie Sanders were Democratic Party candidates. [Pic 2]
Question – Identify whether below events are Independent or Mutually Exclusive?
Event A: Trump winning Republican nomination
Event B: Cruz winning Republican nomination
Event C: Clinton winning Democratic nomination
Event D: Sanders winning Democratic nomination
1. Event A and Event B? (Ans – Mutually Exclusive)
Explanation: Trump and Cruz both belong to same party and hence from one party only one candidate will be nominated for the presidential election. Hence Event A and Event B are mutually exclusive.
2. Event C and Event D? (Ans – Mutually Exclusive)
Explanation: Same reason, both belongs to the same party and hence can be nominated together. Hence Mutually exclusive.
3. Event A and Event C? (Ans – Independent)
Explanation: In first thought, these events look Independent as party nominate their candidate independent to other party nominated candidate. Hence with this reasoning these events are Independent. However sometime Party put some reasoning like which candidate will be stronger against the other party candidate. in this case Party thing if A is nominated from Party one then we will nominate our candidate 1 else if Party one is nominating their candidate B then we will nominate our candidate 2. In this case dependent events and hence Mutually exclusive. But this is not the standard case only occurs with so many permutation combination. Hence we will go with answering these events as Independent.
So that’s all about Probability basics for Data Science. In next post I will be writing about Conditional Probability, Bayes’ Theorem and Probability Distribution which will complete the Probability for Data Science Series.
Recommended Articles:
Feel free to contact us for more details and discussions.
Thanks for the giving awesome information, you are explained very well with the examples of probability in Data Science.Here is another source where you will get more detailed information https://prwatech.in/data-science-training-in-pune/
LikeLiked by 1 person
Thank you.
LikeLike